State and Prove Pythagoras Theorem

11 Mar
Class 10, Math - Class 9 | NCERT, Theorems, , , ,

Pythagoras Theorem

In a right angled triangle, the square of hypotenuse is equal to the sum of squares of the other two sides.

OR

In a right angled triangle, the square of hypotenuse is equal to the sum of squares of perpendicular and base of the triangle.

To Prove

\( \begin{aligned} &BC^2 =AB^2+AC^2\end{aligned}\)

Construction

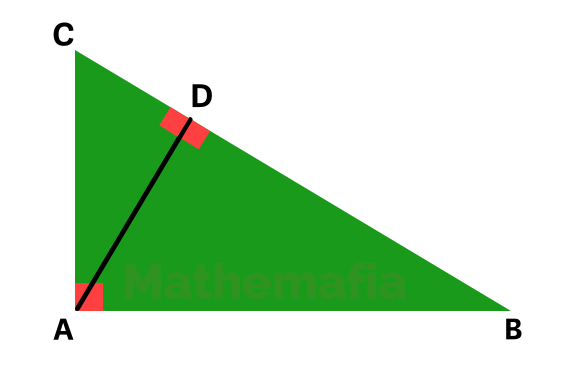
\( \begin{aligned} &\text{Draw } AD \perp BC\end{aligned}\)

Proof

Part 1

\( \begin{aligned} &In \ \ \triangle ABC \text{ and } \triangle ADB \end{aligned}\)
\( \begin{aligned}  &\angle {BAC} = \angle {ADB} = 90^{\circ}\\ &\angle B = \angle B \ \ \ \ \text{(Common)} \end{aligned}\)

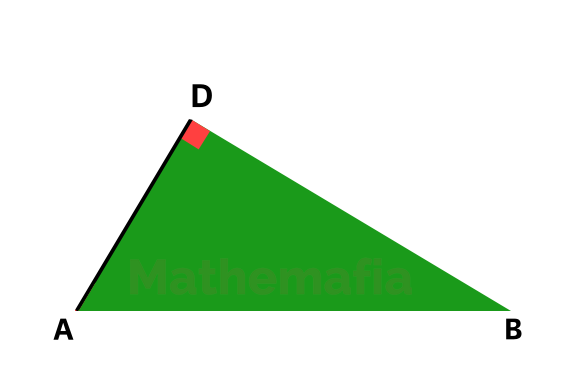
By AA similarity criterion

\( \begin{aligned} &\triangle ABC \sim \triangle DBA \end{aligned}\)

Very Important: We write it as △ABC is similar to △DBA. We cannot write it similar to △ADB even though △DBA and △ADB are same triangles.

Why? Click here to read it or watch the video embedded below.

\( \begin{aligned} &\Rightarrow \frac{AB}{DB} = \frac{BC}{AB}\\\\ &\Rightarrow AB^2 = BC \times DB \ \ …(1)\end{aligned}\)

Part 2

\( \begin{aligned} &In \ \ \triangle ABC \text{ and } \triangle ADC \end{aligned}\)
\( \begin{aligned} &\angle {BAC} = \angle {ADC} = 90^{\circ}\\ &\angle C = \angle C \ \ \ \ \text{(Common)} \end{aligned}\)

By AA similarity criterion

\( \begin{aligned} &\triangle ABC \sim \triangle DAC \end{aligned}\)
\( \begin{aligned} &\Rightarrow \frac{BC}{AC} = \frac{AC}{DC}\\\\ &\Rightarrow AC^2 = BC \times DC \ \ …(2)\end{aligned}\)

Part 3

Adding (1) and (2)

\( \begin{aligned} AB^2+ AC^2 &= BC \times BD + BC \times DC \\ &=BC \times (BD + DC)\\ &=BC \times BC\\ &=BC^2\\ \end{aligned}\)

Hence proved.

Watch on YouTube

Why?

\( \begin{aligned} &\text{Why }\triangle ABC \sim \triangle DBA \text{ but } \triangle ABC \not\sim \triangle ADB\end{aligned}\)

When it comes to similarity and congruence of triangles, students always find it slightly confusing but let me tell you, it is as simple as Virat Kohli hits a six 🏏 at will. All you need is to possess good mathematics skills 😜 like Kohli has (in cricket of-course).

Ok … That’s not true. You don’t need to be as good as Kohli 😜 to understand this concept. 💃🕺 Wow!!! Nacho Nacho. 💃🕺 (If this song can win oscar, one day I will get the Fields Medal. 🏅 🏆 )

Explanation

We just proved that the triangles shown below are similar. The triangles are similar when all three corresponding angles are congruent in both the triangles. In this case:

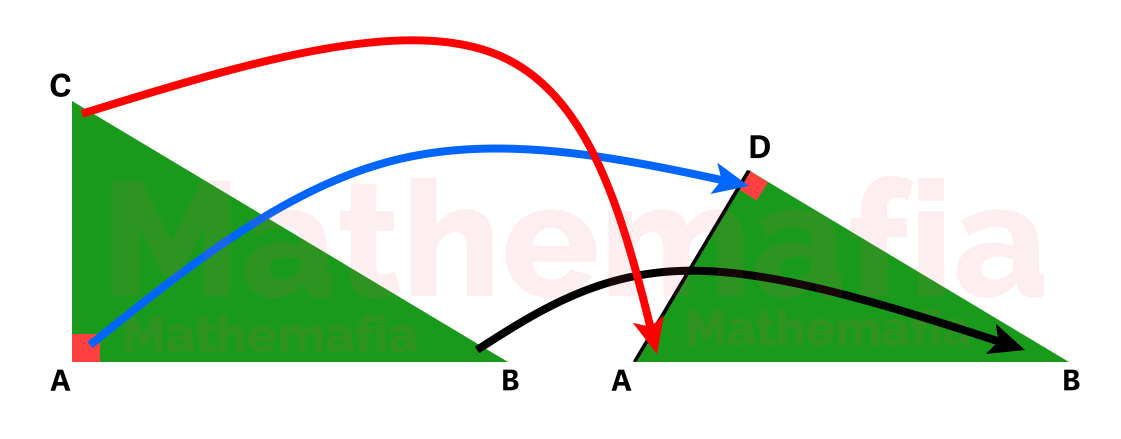
\( \begin{aligned}  \angle {BAC} &= \angle {ADB} = 90^{\circ}\\ \angle B &= \angle B \ \ \ \ \text{(Common)}\\ \Rightarrow \angle {ACB} &= \angle {DAB} \end{aligned}\)

In the picture displayed above you can clearly see mapping of the corresponding angles means the mapping of the corresponding vertices of the two triangles. So while writing the similarity expression, we must write the corresponding vertices in same order on both sides as shown in Mapping Pic. 

Mapping Pic

Welldone Mathemafia 👏💯 !!!

Pytha: Oh my Goras!!! I can’t believe that you have explained it so Beautifully Colorfully. 

Mathemafia: Wow! You struck out Beautifully. 💔